동적프로그래밍
DP, 동적프로그래밍은
하나의 큰 문제를 여러개의 작은 문제로 나눠서 그 결과를 저장하고 다시 큰 문제를 해결할 때 사용하는것으로
특정한 알고리즘이 아닌 하나의 문제해결법이라고 볼 수 있다.
큰 문제를 작은 문제로 쪼개서 , 작은 문제의 답을 저장하고 저장한 답을 이용하여 점점 큰 문제를 해결하면서 저장
한다. 그렇게 원하는 값까지 도달한다.
(기억하며 풀기라고 불리기도 한다.)
DP를 쓰는이유
일반적인 재귀방식 또한 DP와 유사하다.
하지만 일반적인 재귀는 똑같은 작은 문제들을 여러번 계산하게 되서 비효율적이라는것이다.
예를 들어 피보나치 수열을 구하는 재귀의 동작방식을 살펴보자.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 ... 처럼 진행되는 피보나치를
재귀로 구현한다면 return f(n) = f(n-1) + f(n-2) 를 이용하면 될것이다.
하지만 f(n-1) 과 f(n-2)의 동작에서 같은값을 구하는 연산이 많이 반복될것이다.
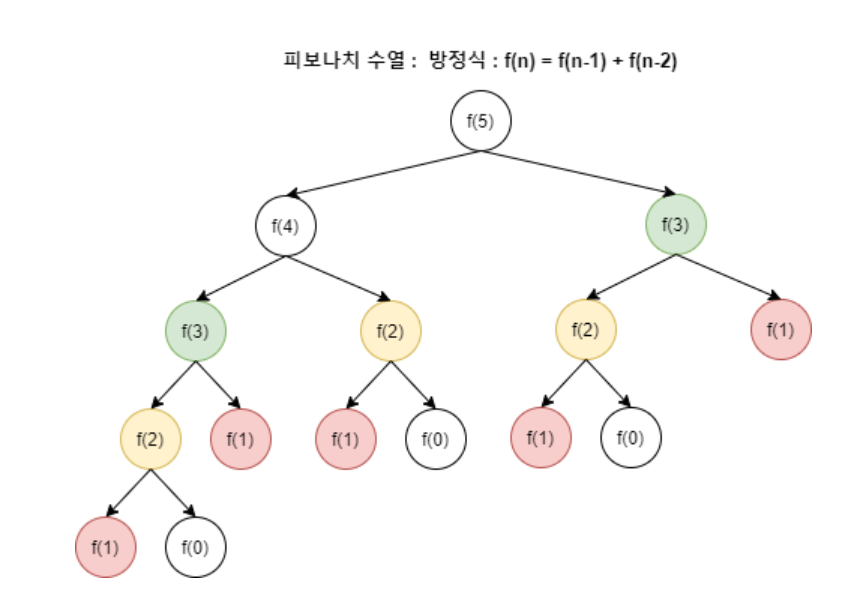
다음과 같이 f(5)의 피보나치값을 구할때 f(5) = f(4) + f(3) 일것이고
그때 f(4) 와 f(3)을 구하는 동작에서 f(2) , f(1) 등 같은 값을 구하는 연산이 많이 생긴다
예시로는 5번째 피보나치이지만 100번째 피보나치일경우 , 쓸모없는 중복연산이 많이생길것이다.
쓸모없는 중복연산을 줄이기위해 한번 구한 작은 값(원하는값을 구하기 위해 구해야하는값)들은 따로 저장해두고
필요할때 꺼내쓰면 된다.
메모이제이션(Memoization)
DP를 구현하는 방법 중 한 종류이다.
한번 구한 결과를 메모리 공간에 메모해두고 , 같은 값을 다시 연산해서 구하지않게 저장된 값을 가져와서 쓰는 기법이다.
DP 사용
1. 중복되는 부분 문제
동일한 작은 문제들이 반복하여 나타나는 경우 ( == 방금 봤던 피보나치 처럼)
-> 계속 사용되는 작은결과들을 저장해두면 연산에 이점이 있을때 사용한다.
피보나치 DP로 구현하기
구현할때 1번째 값과 같은 초기값을 가지는게 중요하다.
long[] fibo = new long[51];
fibo[1] = 1;
fibo[2] = 1;
for (int i = 3; i <= 50; i++) {
fibo[i] = fibo[i - 2] + fibo[i - 1];
}
bw.write(fibo[50] + "");
ㄷ다음과 같이 1,2번째 피보나치값이 1임을 이용하고
피보나치수열의 점화식을 이용해서 3번째부터 ~ 원하는 위치 의 피보나치값을 구할 수있다.
2. 최적 부분 구조
큰 문제를 작은 문제로 나눌 수 있고, 작은 문제의 답을 모아 큰 문제를 해결 할 수 있는 경우
-> 조합문제에서 일반적인 조합을 구현하면 O(2^n)이므로 시간이 많이 소요된다.
그럴때 파스칼의 삼각형을 이용해서 원하는 값까지 삼각형에 값을 채우며 원하는 값을 구하는데
그렇게 큰 값을 구하기 위해 작은값들이 필요하고 , 작은값들을 채워나가면서 큰값을 구할때 사용되는것 같다.
예시)
★백준/11051 이항 계수 2 /조합,BigInteger,파스칼의 삼각형
이항 계수 2 성공 시간 제한메모리 제한제출정답맞힌 사람정답 비율 1 초 256 MB 48877 18134 14257 37.642% 문제 자연수 N\(N\)과 정수 K\(K\)가 주어졌을 때 이항 계수 (NK)\(\binom{N}{K}\)를 10,007로 나눈 나머지
keeeeeepgoing.tistory.com
DP로 푸는 문제파악
어떤상황일때 dp로 푸는것이 좋을까
작은 문제들로 이루어진 하나의 함수로 표현될 수 있는지 -> 점화식을 구할 수 있는가
결국 점화식을 구할 수 있어야한다 (규칙을 찾을 수 있어야한다)
점화식을 이용하여 작은 값들을 저장하고(메모이제이션) 원하는 값을 구한다.
가장 작은 문제의 상태를 알아야한다 -> 피보나치수열에서 1,2번째 피보나치가 1인것과 같이 ( == 기저상태 파악)
점화식의 초기값들을 구할 수 있어야한다. -> 작은문제들을 풀때 사용할것들
1. 문제가 진행되는 규칙을 찾아서 점화식을 구할 수 있는가. (관계식 만들기)
2. 가장 작은 문제의 상태 == 점화식의 초기값들을 얻을 수 있는가. ( 기저상태 파악)
3. 1,2번을 구했다면 작은 문제들부터 값을 저장하면서 원하는값이 나올때까지 전진한다. ( 메모이제이션)
DP 구현방법
중요한 팁 : dp배열의 크기는 최댓값(최악의 경우)로 설정해둔다.
이유 : dp배열을 전역변수로 지정해놨기에 재활용가능 ,
즉 테스트케이스가 여러개일때 연산수를 줄일 수 있음,
n이 1일때의 인덱스오류를 걱정안해도된다.
예시)
백준/1904 01타일 / 다이나믹 프로그래밍 + 제출전 최악의경우값들 넣어보기 + dp배열의 크기는 나
01타일 성공 시간 제한메모리 제한제출정답맞힌 사람정답 비율 0.75 초 (추가 시간 없음) 256 MB 75477 24571 19491 31.851% 문제 지원이에게 2진 수열을 가르쳐 주기 위해, 지원이 아버지는 그에게 타일들
keeeeeepgoing.tistory.com
1. 바텀업 (Bottom-up) 방식
이름에서 알 수 있듯이 , 아래에서부터 계산을 수행하고 누적시켜서 전체 큰 문제를 해결하는 방식이다.
작은값들을 저장하기위해(메모이제이션) dp 배열을 생성하고 dp배열이 1차원배열이라고 가정하고
dp[0]가 기저 상태이고 , dp[n]을 목표값이라고 하자.
Bottom-up 방식은 dp[0] 부터 시작하여 반복문을 통해 점화식으로 결과를 내서 dp[n]값 까지 구하는 방식이다.
(기저값을 이용하여 작은값들을 저장, 저장한 값을 사용해서 다음값을 구하고 전진해서 원하는값을 구하는 방식이다.)
바텀업 방식으로 피보나치 구현
public static long bottomUp(int n) {
long[] fibo = new long[51];
fibo[1] = 1;
fibo[2] = 1;
for (int i = 3; i <= 50; i++) {
fibo[i] = fibo[i - 2] + fibo[i - 1];
}
return fibo[n];
}기저상태의 값을 사전에 미리 저장하고,
기저상태 다음값부터 구해서 저장하는 방식이다.
---(저장된 값을 이용해서 그 다음값을 구하는것을 반복한다) ----
2. Top-Down 방식
위에서 부터 내려가는 방식으로
dp[n]의 값을 찾기 위해 위에서부터 재귀적인 호출을 시작하서 dp[0]의 기저상태(최초값)까지 내려간 다음
해당 결과 값을 재귀를 통해 전이시켜 재활용하는 방식이다.
탑 다운 방식으로 피보나치 구현
static long[] fibo;
public static void main(String[] args) throws IOException {
int n = Integer.parseInt(br.readLine());
fibo = new long[n];
bw.flush();
bw.close();
}
public static long topDown(int n) {
if (n == 1 || n == 2) {
return 1;
}
if (fibo[n]== 0) { // 값이 저장되어있지않다면 값을 구해서 넣어준다. -> 값을 구하기위해 기저상태까지 내려갈것이다.
fibo[n] = topDown(n - 2) + topDown(n - 1); // 값을 저장한다.
}
return fibo[n]; // 값이 이미 저장됬거나(메모이제이션), 이미 위에서 값을 구해서 저장된 값을 리턴
// 리턴하면서 재귀적으로 값들이 전이되고 결국에는 원하는값을 리턴하게된다.
}
}
따로 떼어서 보면
public static long topDown(int n) {
if (n == 1 || n == 2) {
return 1;
}
if (fibo[n]== 0) { // 값이 저장되어있지않다면 값을 구해서 넣어준다. -> 값을 구하기위해 기저상태까지 내려갈것이다.
fibo[n] = topDown(n - 2) + topDown(n - 1); // 값을 저장한다.
}
return fibo[n]; // 값이 이미 저장됬거나(메모이제이션), 이미 위에서 값을 구해서 저장된 값을 리턴
// 리턴하면서 재귀적으로 값들이 전이되고 결국에는 원하는값을 리턴하게된다.
}동작방식 : (dp배열 -> fibo배열)
n을 50이라고 했을때
값이 저장된게 없으니까 if문 안에 fibo[n] = topDown(n - 2) + topDown(n - 1); 가 실행될것이다.
fibo[50] = topDown(48) + topDown(49) 이므로
맨앞의 topDown(48)이 먼저 실행된다.
저장된 피보값들이 없으니 기저상태값까지 내려간다 (n==1 , n==2)
그리고 난후 return 되면서 fibo[3] , fibo[4], .....등 값을 리턴하면서 fibo라는 dp배열에 값을 저장할것이다.
그렇게 fibo[48]은 48까지 올라면서 저장된 fibo [47] 과 fibo[46]값에 의해 구해지고 fibo[48]또한 저장된다.
그리고 난후
fibo[50] = topDown(48) + topDown(49) 에서
topDown(48)이 실행 될텐데
fibo[48] 를 구할때 사용되는 fibo[47] fibo[46]은 이미 앞에서 구해서 저장해놨기 때문에
중복되는 연산을 다시 할 필요없이 값이 구해진다.
탑다운,바텀업 예시문제
https://keeeeeepgoing.tistory.com/97
백준/1010 다리놓기
다리 놓기 성공 시간 제한메모리 제한제출정답맞힌 사람정답 비율 0.5 초 (추가 시간 없음) 128 MB 64625 29963 24502 48.438% 문제 재원이는 한 도시의 시장이 되었다. 이 도시에는 도시를 동쪽과 서쪽으
keeeeeepgoing.tistory.com
다른 예시
★백준/11051 이항 계수 2 /조합,BigInteger,파스칼의 삼각형
이항 계수 2 성공 시간 제한메모리 제한제출정답맞힌 사람정답 비율 1 초 256 MB 48877 18134 14257 37.642% 문제 자연수 N\(N\)과 정수 K\(K\)가 주어졌을 때 이항 계수 (NK)\(\binom{N}{K}\)를 10,007로 나눈 나머지
keeeeeepgoing.tistory.com
출처,더 자세한정보
알고리즘 - Dynamic Programming(동적 계획법)
1. 개요 DP, 즉 다이나믹 프로그래밍(또는 동적 계획법)은 기본적인 아이디어로 하나의 큰 문제를 여러 개의 작은 문제로 나누어서 그 결과를 저장하여 다시 큰 문제를 해결할 때 사용하는 것으로
hongjw1938.tistory.com
'자바 > 알고리즘' 카테고리의 다른 글
| [Java] DFS, BFS (0) | 2022.12.20 |
|---|---|
| [Java] 그리디 알고리즘 (Greedy Algorithm) , 탐욕 알고리즘 (0) | 2022.12.20 |
| [Java] 이분탐색 ,이진탐색 (0) | 2022.12.07 |
| [Java] 재귀 [미완] (0) | 2022.12.05 |
| 순열,중복순열,조합,중복조합 정리 (1) | 2022.10.17 |


댓글